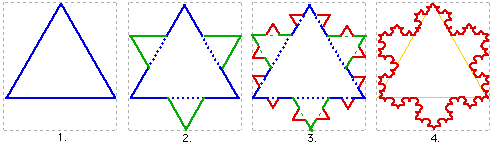
- Start with an equilateral triangle whose sides have length 1.
- On the middle third of each of the three sides, build an equilateral triangle with sides of length 1/3. Erase the base of each of the three new triangles.
- On the middle third of each of the twelve sides, build an equilateral triangle with sides of length 1/9. Erase the base of each of the twelve new triangles.
- Repeat the process with this 48-sided figure. See the likeness to a crystal of snow emerge?

At the right, figure 4 is magnified by a power of two.
The “limit curve” defined by repeating this process an infinite number of times, adding more and more, smaller and smaller triangles at each stage, is called the Koch’s SNOWFLAKE CURVE, named after Niels Fabian Helge von Koch (Sweden, 1870-1924).
The snowflake curve has some interesting properties that may seem paradoxical.
- The snowflake curve is connected in the sense that it does not have any breaks or gaps in it. But it’s not smooth (jagged, even), because it has an infinite number of sharp corners in it that are packed together more closely than pebbles on a beach.
- The snowflake never escapes the dashed square you see in figures 1-4, so it encloses a finite amount of area no larger than a credit card. On the other hand, at each step building the new little triangles adds more than one unit of length to the curve. To be precise, [4 ÷ 3]n – 1 units are added at the nth step, so the length of the snowflake is larger than 3 + 1 + 1 + 1 + 1 + 1 + ……. = infinity. The snowflake curve is infinitely long, yet it would fit in your wallet!
- Under a magnifying glass, a little piece of the snowflake looks identical to a larger, unmagnified chunk. Objects that exhibit this kind of self-similarity are called FRACTALS and are of great research and applied interest in modern science and mathematics.
Last Updated February 7, 2022